What is the Greater Than or Equal To Symbol?
Have you ever wondered about the mysterious “≥” symbol you sometimes encounter in math problems and wanted to know more about its meaning and uses?
You’re in luck! This powerful symbol, the Greater Than or Equal To symbol, may seem daunting at first glance. Still, it’s an essential key to solving many mathematical problems.
From basic definitions to advanced applications, your journey into the Greater Than or Equal To symbol starts here. Keep reading, and your mathematical prowess is sure to grow!
Let’s get started!
Fast Facts
≥
Greater Than or Equal To Symbol
Greater Than or Equal To Symbol (≥) Overview
Here’s a table that outlines various technical details about the Greater Than or Equal To symbol (≥):
| Attribute | Detail |
|---|---|
| Symbol Name | Greater Than or Equal To |
| Unicode | U+2265 |
| Image | ≥ |
| Brief Description | Used to indicate that a value is greater than or equal to another value. |
| Unicode Version and Date | Unicode 1.1; June 1993 |
| Unicode Block Name | Mathematical Operators |
| Plane | Basic Multilingual Plane (BMP) |
| Script | Common |
| Category | Symbol, Math |
| Bidirectional Class | Other Neutrals (ON) |
| Combining Class | 0 (Not Reordered) |
| Character is Mirrored | No |
| HTML Entity | ≥ or ≥ |
| CSS | \2265 |
| UTF-8 Encoding | 0xE2 0x89 0xA5 |
| UTF-16 Encoding | 0x2265 |
| UTF-32 Encoding | 0x00002265 |
| ASCII Code | Not applicable (symbol is outside the ASCII range) |
Here’s What You Will Find
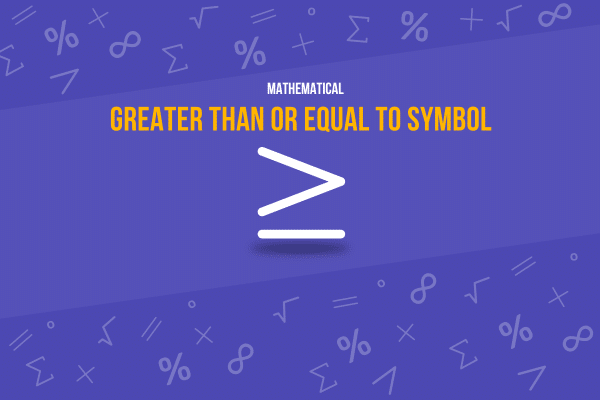
Greater Than or Equal To Symbol
The Greater Than or Equal To symbol (≥) is a fundamental mathematical symbol that denotes a relationship between two quantities. It expresses that the value on the left side of the symbol is either larger than or equivalent to the value on the right side.
For example, seven is greater than five if we write 7 ≥ 5. Similarly, if we write 3 ≥ 3, three equals three.
Other Names
The Greater Than or Equal To symbol (≥) also goes by several other names in various contexts. In mathematical terminology, it’s often called the “inequality symbol” because it denotes an inequality relationship between two values.
In programming languages and computing, you might hear it referred to as the “comparison operator,” as it’s commonly used to compare the values of two expressions. It is also sometimes called the “more than or equal to symbol.” Regardless of the name, the meaning stays the same: it indicates that one quantity is larger than or equal to another.
Greater Than or Equal To Symbol Meaning
The Greater Than or Equal To symbol (≥) is a fundamental mathematical symbol used to denote that the value on the left side of the symbol is either greater than or equal to the value on the right side. This symbol is pivotal in mathematical expressions and equations, serving as a concise and clear method for expressing relational conditions between two quantities or variables.
The Greater Than or Equal To symbol (≥) is a binary relation symbol that communicates an inequality between two quantities. When placed between two values, it asserts that the quantity or expression on the left is greater than or equal to the one on the right.
Understanding this symbol is crucial for conveying complex mathematical relationships succinctly and clearly. Whether comparing numbers, defining a range of possible solutions to an equation, or establishing the conditions under which a mathematical statement is true, the Greater Than or Equal To symbol is an indispensable tool in mathematics and related fields.
Symbolism of the Greater Than or Equal To Symbol
The Greater Than or Equal To symbol (≥) encapsulates deep symbolic meanings beyond its straightforward mathematical application. Here are some key symbolic representations of this symbol:
- Concept of Sufficiency: At its core, the symbol represents sufficiency and adequacy, signifying that a quantity meets or exceeds a certain benchmark. Meeting a standard is crucial in various settings, including educational assessments and economic evaluations.
- Themes of Equality and Fairness: The symbol frequently symbolizes equality and fairness, promoting equivalence and the possibility of exceeding established norms. This is particularly resonant in discussions around social justice and educational equity, where it might symbolize the aim for all individuals to reach at least a baseline level of opportunity or achievement.
- Motivational Use: In motivational contexts, the symbol encourages setting foundational standards while striving for greater accomplishments. It serves as a prompt for ambition, suggesting that one should not only meet the minimum requirements but aim to surpass them.
- Legal and Regulatory Significance: The symbol denotes that practices or products meet or exceed the necessary standards in compliance and regulation. It symbolizes adherence to and surpassing regulatory benchmarks, which are crucial in safety, health, and quality control.
- Artistic and Cultural Interpretations: The symbol can also appear in cultural and artistic expressions, conveying overcoming obstacles, reaching for higher achievements, and continuous growth. It becomes a metaphor for progression, improvement, and the relentless pursuit of excellence, embodying the dynamic of never settling for less.
Each of these points highlights how the Greater Than or Equal To symbol serves as a powerful icon in various facets of life, from the academic and professional worlds to personal and cultural dimensions.
Greater Than or Equal To Symbol Unicode
Unicode is a universal character encoding standard used in computing that assigns a unique number to every character, regardless of platform, program, or language. It covers all the characters for writing systems worldwide, modern and ancient. It also includes technical symbols, punctuations, and many other characters used in writing text.
The Unicode standard ensures that computer systems can display text accurately and consistently, making digital communication more efficient and accessible across different languages and regions.
For the Greater Than or Equal To symbol (≥), the Unicode is U+2265. This code tells the computer to render this specific mathematical symbol. Using this Unicode, you can accurately represent the symbol in various applications that support the Unicode standard, even if your keyboard does not have a specific key.
Greater Than or Equal To Symbol Uses
The Greater Than or Equal To symbol (≥) is versatile, finding application across various fields beyond mathematics. Here are some of the primary uses of this symbol:
Mathematics
- Inequalities: It is extensively used to express inequalities where one quantity is not less than another.
- Calculus: Utilized to define limits and continuity conditions.
- Optimization Problems: Helps specify constraints and values that must be satisfied in operations research and economic models.
Computer Programming
- Conditional Statements: Fundamental in programming for making comparisons and decisions based on variable values.
- Loops and Control Structures: Ensures that loops continue as long as a condition remains true or until it becomes false.
Statistics
- Hypothesis Testing: Used to define the rejection region in statistical tests, indicating that a statistic is greater than or equal to a certain critical value.
- Confidence Intervals: Helps denote the minimum value of a parameter estimate within a given confidence level.
Education
- Grading Systems: Teachers and professors might use it to set benchmarks for grades, specifying the minimum score needed to achieve a certain grade.
- Assessment Criteria: Establishes thresholds for passing tests or qualifying for advanced levels of study.
Economics and Finance
- Economic Models: Used to express conditions under which economic equilibrium is maintained or a market remains stable.
- Financial Analysis: Financial modeling helps define break-even points and safety margins.
Science and Engineering
- Engineering Specifications: Engineers use it to denote minimum design requirements or tolerances that must be met or exceeded.
- Scientific Research: Specifies thresholds where certain conditions must be observed in experimental protocols.
Everyday Use:
- Decision-Making: This symbol might be used in personal decision-making tools, like spreadsheets for budgeting or planning, to ensure certain criteria are met.
- DIY Projects: In instructions for various projects, ensuring measurements or quantities meet specified minimums.
This symbol is critical in numerous disciplines, helping professionals and individuals articulate and effectively enforce standards, thresholds, and criteria. Whether in academic, professional, or personal contexts, the Greater Than or Equal To symbol is integral in facilitating clear, precise, and logical decision-making and evaluations.
The Greater Than or Equal To symbol (≥) is multifaceted, playing a vital role across various disciplines. In mathematics, it’s extensively used in algebraic inequalities and number lines to signify that one quantity is larger than or the same as another. It’s also used to define domain restrictions and interval notations. In statistics, it comes into play while expressing confidence intervals, cumulative distribution functions, and describing hypotheses for hypothesis testing.
In computer programming and logic, the symbol is a comparison operator for creating logical conditions. In finance and business, it’s used for breakeven analysis and to represent limits in economic models. By understanding this symbol, one gains a great utility tool capable of unlocking advanced mathematical concepts and problem-solving strategies.
Greater Than or Equal To Symbol Examples
The Greater Than or Equal To symbol (≥) is widely used in various practical scenarios to communicate thresholds, limits, and requirements. Here are several illustrative examples that show the symbol in action across different contexts:
Academic Testing
- Score Requirements: A university may stipulate that applicants must have a GPA ≥ 3.5 to qualify for a scholarship program.
- Test Cut-offs: A passing mark might be set in standardized testing, so students need scores ≥ 70% to advance or pass.
Economic Analysis
- Market Studies: Economists might analyze data to identify cases where product demand ≥ exceeds supply and potential shortages.
- Income Studies: Researchers could set criteria in their studies so that only individuals with an income ≥ $50,000 are included in an analysis of economic behavior.
Programming and Software Development
- User Access Levels: In a software application, access to certain features might be restricted to users with a security clearance level ≥ 4.
- Resource Allocation: A script may ensure that a process continues to run only if the system memory available is ≥ 512 MB.
Health and Medicine
- Medical Thresholds: A medical guideline might state that a specific medication is recommended for patients with a blood pressure reading ≥ 140/90 mmHg.
- Dietary Recommendations: Nutritional guidelines could recommend that adults consume ≥ 5 servings of fruits and vegetables daily.
Engineering and Construction
- Material Specifications: Building codes might require a concrete mix to have a strength ≥ 5,000 psi to ensure safety and durability.
- Safety Standards: Regulations may dictate that personal protective equipment must meet specific standards, such as resistance ≥ a certain threshold, which is mandated for industry compliance.
Retail and Commerce
- Discount Eligibility: A store promotion might offer a discount on purchases of ≥ $100.
- Shipping Policies: To encourage bulk purchases, free shipping might be offered on orders with a total weight of more> than 20 kg.
Environmental Studies
- Pollution Levels: Environmental regulations might impose fines on factories where emissions of certain pollutants are ≥ permitted levels.
- Resource Management: Water usage advisories might be issued when reservoir levels are ≥ 80% capacity, indicating sufficient water supply.
These examples illustrate how the Greater Than or Equal To symbol helps set clear, quantifiable standards across many sectors, aiding in decision-making processes by establishing definitive benchmarks that must be met or exceeded.
Why is the Greater Than or Equal To Symbol Important?
The Greater Than or Equal To symbol (≥) is highly important due to its wide-ranging application and utility in numerous fields. This seemingly simple symbol plays an integral role in mathematical reasoning, allowing us to succinctly express a range of values and conditions. By enabling us to formulate and solve inequalities, it broadens our capacity to understand and describe complex relationships between quantities.
It’s also vital for coding logic in computer programming, facilitating conditional statements that drive algorithm behavior. Moreover, it’s essential for describing phenomena, formulating models, and conducting analyses in fields like economics, finance, and statistics.
Thus, the symbol underpins many aspects of academic knowledge and practical problem-solving, making it a fundamental part of mathematical literacy.
History of the Greater Than or Equal To Symbol
The Greater Than or Equal To symbol (≥) has an interesting history that traces back to the development of mathematical notation over several centuries. Understanding its origins provides insight into how mathematical communication has evolved to become more precise and efficient.
- Early Developments:
The roots of the symbol begin with the basic “greater than” (>) and “less than” (<) symbols, which were first used by Thomas Harriot, an English mathematician, in his book “Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas,” published posthumously in 1631. Harriot’s work laid the groundwork by introducing these symbols to express simple inequalities. - Evolution of the Symbol:
The adaptation to include an equality component (≥, ≤) came much later. This modification was influenced by the need to succinctly express “not less than” or “not greater than” in mathematical writing, which was especially useful in formal proofs and algebraic reasoning. The precise introduction of these combined symbols isn’t as well-documented as with basic mathematical symbols. Still, they were in regular use by the 19th century, reflecting the maturation of algebra as a discipline. - Standardization in Modern Mathematics:
By the 20th century, the symbols were standardized and universally recognized in the mathematical community. Their inclusion in textbooks and academic papers helped solidify their role in mathematical notation. The formalization of mathematical logic and set theory during this period also played a crucial role in embedding these symbols into the fabric of mathematical language. - Technological Adoption:
With the advent of computers and digital typesetting in the late 20th century, the Greater Than or Equal To symbol was incorporated into Unicode, ensuring that it could be easily used in digital communication and programming. This step was crucial for the symbol’s use in software development, data analysis, and online educational resources.
The history of the Greater Than or Equal To symbol reflects broader trends in the development of mathematical notation, where the goal has consistently been to enhance clarity, precision, and efficiency in written mathematics. This symbol not only facilitates greater understanding and communication within the field but also serves as a bridge connecting ancient mathematical practices to modern computational needs.
Origin of the Greater Than or Equal To Symbol
The origin of the Greater Than or Equal To symbol (≥) is an intriguing narrative within the history of mathematical notation, closely linked to the evolution of inequality symbols used to express complex relationships between numbers.
- Inception of Inequality Symbols:
The foundational symbols for inequalities, specifically the “greater than” (>) and “less than” (<), were introduced by Thomas Harriot, an English mathematician, in his manuscript “Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas,” which was published posthumously in 1631. Harriot’s symbols were designed to show simple numerical relationships clearly and succinctly. - Development of Combined Symbols:
While Harriot introduced the basic concepts of comparison, the addition of the equality line to create the symbols for “greater than or equal to” (≥) and “less than or equal to” (≤) evolved separately. The modification to include equality emerged as mathematicians sought more comprehensive tools to express strict and non-strict inequalities within a single notation. This adaptation allowed for more versatile expressions in mathematical proofs and equations. - Formal Introduction and Use:
The combined symbols were first seen in print during the 19th century as the practice of algebra became more refined and widespread. Although it is not attributed to a single individual, the adaptation reflects a natural progression in mathematical notation aiming to enhance expressiveness and precision. By the late 19th and early 20th centuries, these symbols had become a standard part of the mathematical lexicon, appearing in educational materials and professional publications. - Adoption Across Fields:
As mathematics continued to influence other fields, such as economics, engineering, and the emerging computer sciences, the utility of these symbols expanded. Their adoption of programming languages and software applications further solidified their importance, making them indispensable in academic and practical applications.
The origin of the Greater Than or Equal To symbol is a testament to the dynamic nature of mathematical language. It highlights how symbols evolve to meet the needs of communication clarity and logical expression in mathematics. This symbol, while simple, represents a significant leap in the ability to convey complex mathematical relationships efficiently.
Evolution of the Greater Than or Equal To Symbol
The Greater Than or Equal To symbol (≥) has remained fairly consistent in its representation and meaning since its inception in the 19th century. Its main evolution has been in its expanded application across a broader range of disciplines and contexts.
Originally employed primarily in pure mathematics to express inequalities, it has spread to other areas, such as computer programming, where it’s used as a comparison operator in algorithms and conditional statements.
Furthermore, with the advent of Unicode, a standardized character encoding system, the symbol is now universally recognized and used in digital platforms across different languages and regions. This standardization ensures that the symbol is consistently displayed and understood, promoting clear and accurate communication in the digital world.
Greater Than or Equal To Symbol In Everyday Life
Reflecting on the Greater Than or Equal To symbol (≥), one can appreciate its profound universality and flexibility. Just as it’s used in mathematics to compare quantities or establish a range of acceptable solutions, its principles can also be applied in everyday life. For instance, consider time management. You might decide to devote ≥2 hours per day to a personal project, implying that two hours is your baseline, but you’re open to spending more time if available.
Or perhaps when grocery shopping, you set a budget such that your total spending is ≤$100, ensuring you don’t exceed your financial limits. The symbol can even be employed metaphorically in personal development, reminding us to always strive to be “greater than or equal to” the challenges we face and to continually learn and grow to meet new obstacles with confidence.
Last Thoughts
The Greater Than or Equal To symbol has proven to be more than just a collection of lines and curves. Its fundamental role in mathematics and its expansive reach into numerous other fields underlines its importance and universal applicability. As you’ve journeyed through this fascinating symbol’s meaning, history, uses, and cultural influences, we hope it has sparked curiosity and appreciation for the power of mathematical symbols.
Don’t stop here, though! There’s a myriad of other symbols and signs waiting to be explored. Who knows, you might just find a new favorite symbol or even some cool merchandise that showcases your newfound interest.
Continue on your journey of discovery, and remember, every symbol has a story.
Before You Go
Now that you’ve explored the depths of the Greater Than or Equal To symbol, why not embark on a new adventure? There’s a world of intriguing symbols waiting to be discovered, each with unique story and applications, ready to deepen your understanding of mathematics and beyond.
If you found this exploration of the Greater Than or Equal To symbol (≥) insightful, why not share it with others? Whether they’re fellow math enthusiasts, students tackling inequalities, or professionals seeking to enhance their technical skills, this information could illuminate a small but significant part of their academic or professional journey.
Sharing this post can help spread knowledge and perhaps spark curiosity or a deeper appreciation for the world of mathematical symbols.
So, go ahead and share this with your network on social media, in educational forums, or within your professional community!